Résoudre le problème du sac à dos
Le problème du sac à dos est un problème d'optimisation qui consiste à trouver un lot d'objets de valeur maximale qui tienne dans un sac de capacité limitée. Plus précisément, une instance de ce problème est la donnée :
- - d'un entier P_max qui donne le poids maximal que peut contenir le sac ;
- - d'un entier n qui donne le nombre d'objets ;
- - d'un entier p_k qui donne le poids de l'objet numéro k, et ce pour chaque k entre 0 et n-1 ;
- - d'un entier v_k qui donne la valeur de l'objet numéro k, et ce pour chaque k entre 0 et n-1.
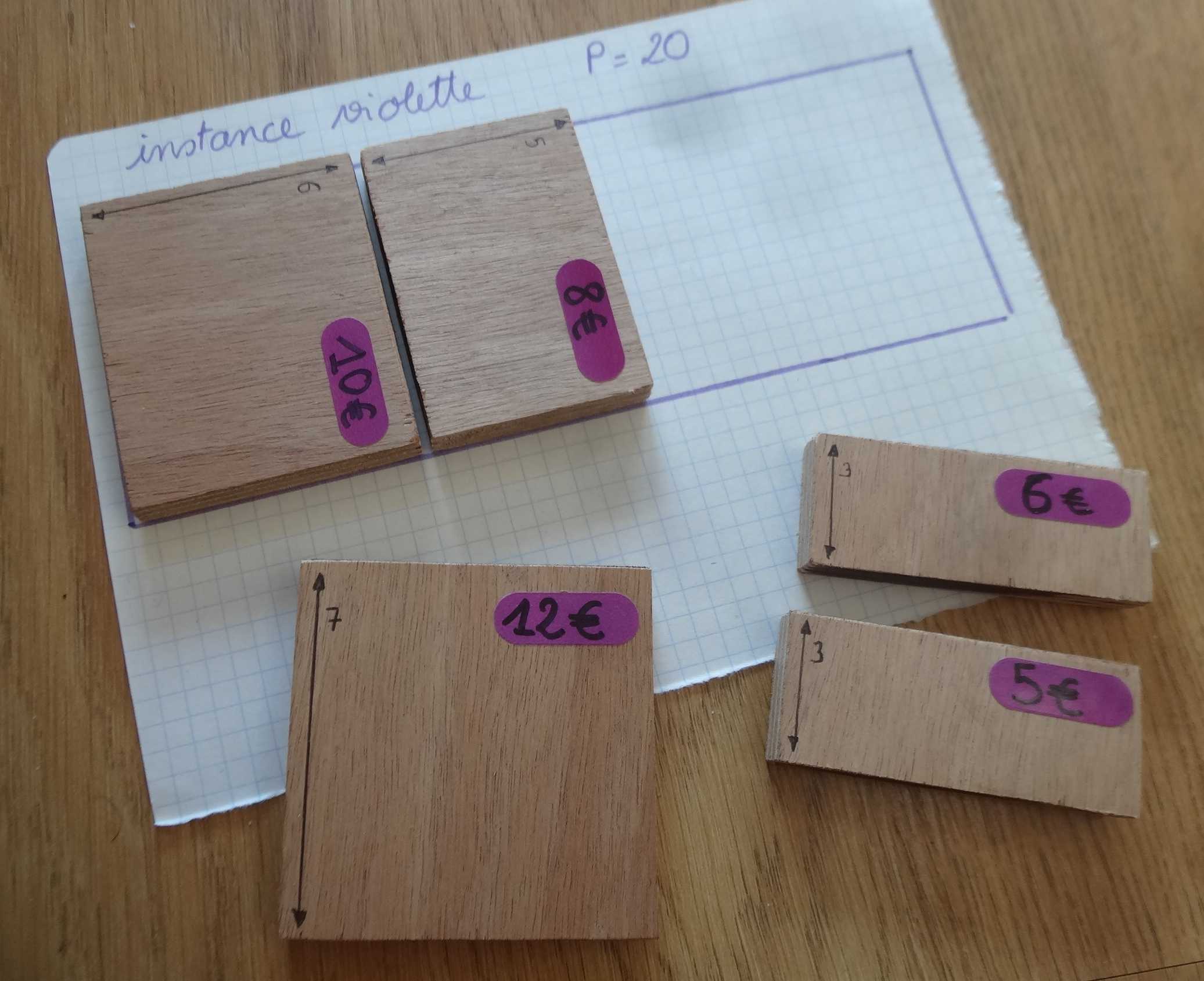
La photo ci-dessous montre une instance à cinq objets fabriquée pour être manipulée lors des ateliers de la Fête de la Science. En numérotant ces cinq objets de façon arbitraire, cette instance correspond aux valeurs suivantes :
- - P_max = 20 ;
- - n = 5 ;
- - p_0 = 3 et v_0 = 5 ;
- - p_1 = 3 et v_1 = 6 ;
- - p_2 = 5 et v_2 = 8 ;
- - p_3 = 6 et v_3 = 10 ;
- - p_4 = 7 et v_4 = 12.
Ce problème est connu pour être un problème NP-difficile, c'est-à-dire qu'on ne connaît pas d'algorithme de complexité polynomiale résolvant ce problème. Néanmoins on peut résoudre ce problème sur de petites instances en utilisant de la programmation dynamique.
Pour établir cet algorithme, on raisonne par disjonction de cas : "je prends ou je ne prends pas l'objet numéro k dans le sac ?".
Lorsque j'ai un seul objet à disposition, la réponse est simple : s'il tient dans le sac, c'est-à-dire si p_k ⩽ P, je le prends et j'ai un lot de valeur v_k, sinon je ne peux pas le prendre, et j'ai un lot de valeur 0.
Lorsque j'ai à disposition des objets numérotés de 0 à k avec k>0, la meilleure valeur que je peux obtenir pour un sac de capacité P est le maximum entre
- - la meilleure valeur en utilisant les objets numérotés de 0 à k-1 pour un sac de capacité P ;
- - la valeur de l'objet k + la meilleure valeur en utilisant les objets numérotés de 0 à k-1 pour un sac de taille (P- la taille de l'objet k), pourvu que l'objet numéro k tienne dans le sac.
Considérons (P_max, n, p, v) une instance du problème. Pour chaque entier k entre 0 et n-1, et pour chaque entier P entre 0 et P_max, on note A(k,P) la meilleure valeur en utilisant les objets numérotés de 0 à k pour un sac de taille P. Les remarques précédentes se traduisent alors par la relation de récurrence suivante.
- - Si k = 0 et p_0 > P, alors A(k,P) = 0.
- - Si k = 0 et p_0 ⩽ P, alors A(k,P) = v_0.
- - Si k > 0 et p_k > P, alors A(k,P) = A(k-1,P).
- - Si k > 0 et p_k ⩽ P, alors A(k,P) = max( A(k-1,P), v_k + A(k-1,P-p_k) ).
On peut appliquer cet algorithme à la main en remplissant un tableau à n fois (P_max + 1) cases.
J'ai préparé des tableaux à imprimer (trois par feuilles) pour les cinq objets violets présentés ci-dessus.
tableau avec détail pour P_max = 8
tableau sans détail pour P_max = 12
Le code en OCaml ci-dessous implémente cet algorithme (en parlant de hauteur au lieu de poids, ce qui ne change rien).
type valeur = int
type objets = hauteur array * valeur array
let objets_violets : objets =
[| 3; 3; 5; 6; 7|],
[| 5; 6; 8; 10; 12|]
let prog_dyn_sac_a_dos ((th,tv): objets)(h_max: hauteur): valeur =
let n = Array.length th in
assert (Array.length tv = n);
let tab = Array.make_matrix (n) (h_max+1) 0 in
(*tab k h donnera la valeur maximale d'un lot d'objets d'indice
entre 0 et k pour un sac de hauteur h *)
for h = 0 to h_max do
if th.(0) <= h then tab.(0).(h) <- tv.(0) else ()
done;
for k = 1 to n-1 do
(* tab.(k).(0) = 0, déjà initialisé *)
for h = 0 to h_max do
if th.(k) <= h
then
let avec = tv.(k) + tab.(k-1).(h-th.(k)) in
let sans = tab.(k-1).(h) in
tab.(k).(h) <- max avec sans
else
tab.(k).(h) <- tab.(k-1).(h)
done
done;
tab.(n-1).(h_max)
let resoud_violette = prog_dyn_sac_a_dos objets_violets
Ce code peut être testé en ligne en utilisant TryOCaml ou bien basthon.
Dans les deux cas, il faut :
- -> copier le code source ci-dessus dans l'éditeur à gauche ;
- -> l'évaluer (bouton "exécuter" sur basthon) ;
- -> appeler la fonction "resoud_violette" dans la console à droite.
On peut tester pour différentes tailles de sac et ainsi vérifier que l'on a bien rempli le tableau à la main. On peut aussi laisser ce code en OCaml de côté, ouvrir basthon en mode Python et essayer de recoder cet algorithme.