
Page personnelle de Maxime BOUCHEREAU

Sur cette page se trouvent divers documents et petits projets personnels qui ne sont pas en lien avec l'enseignement ou la recherche. Vous y trouverez beaucoup de simulations numériques.
Le jeu des échelles et serpents est un jeu de société bien connu, qui consiste à atteindre le plus rapidement possible la dernière case du plateau en avançant d'un certain nombre de cases donné par un lancé de dé. Toutefois, lorsque l'on tombe sur une queue de serpent après un lancé de dé, on doit descendre jusqu'à la tête. Inversement, le fait d'arriver au pied d'une échelle à l'issue d'un lancé de dé permet de monter jusqu'au sommet de l'échelle. Le côté mathématique du jeu réside dans le fait qu'il est possible de le modéliser par une chaîne de Markov, ce qui permet d'étudier le nombre moyen de lancés de dés nécessaires à ce qu'une certaine proportion des joueurs puisse terminer la partie. Une partie peut-être générée via ce code Python.
Traditionnellement, un plateau comporte 100 cases (10 x 10), mais il est tout à fait possible de diminuer le nombre de cases. Ici, nous avons simulé une partie de 500 joueur.euse.s sur un plateau de 100 cases, où environ 40 lancers de dés sont nécessaires pour que 90% des joueur.euse.s terminent la partie, ce que montrent à la fois l'étude théorique par chaîne de Markov et l'évolution de la partie. Sur une autre simulation, nous avons simulé une petite partie de 20 adversaires sur un plateau de 16 cases, terminée en une dizaine de lancés.
Il est également bien entendu possible d'augmenter le nombre de cases du plateau. Sur la première simulation, nous avons fait s'affronter 1000 joueur.euse.s sur un plateau de 225 cases. Plus grand encore, sur la deuxième simulation, 2000 adversaires s'affrontent sur un plateau de 400 cases. Dans ce dernier cas, l'étude théorique par chaîne de Markov (confirmer par la simulation numérique) montre qu'il faut plus de 200 lancés de dés pour que 90% des adversaires terminent la partie.
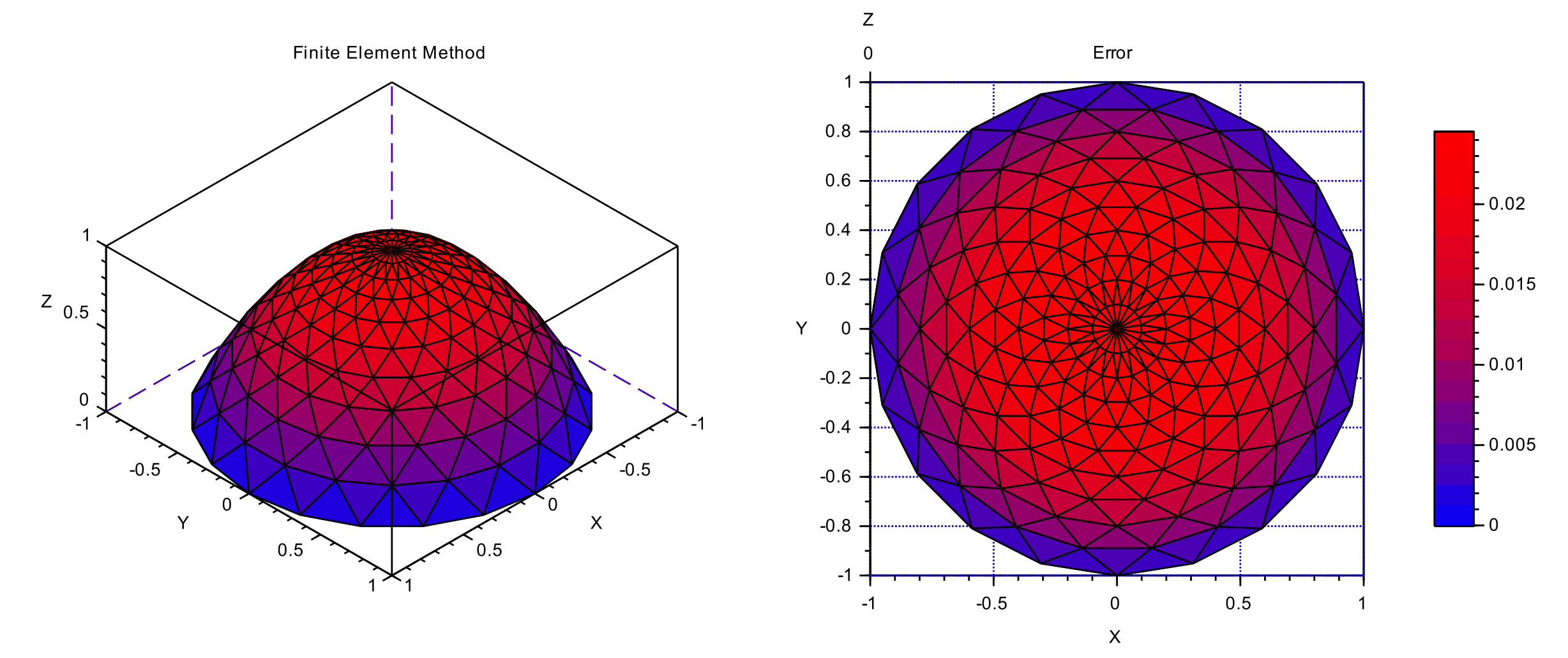
Ce projet présente la méthode des éléments finis de Lagrange en deux dimension d'espace en introduisant le principe de cette méthode, puis l'équation de Poisson est étudiée. Des résultats de convergence sont ensuite illustrés via des simulations numériques.
Voici les documents associés au projet:
On s'intéresse à l'équation différentielle stochastique dVt = - ∇ V(Vt) dt + σ dBt (amélioration de l'équation de Langevin), où Vt est la vitesse d'une particule et (Bt)t désigne le mouvement brownien. La vitesse d'une particule étant donnée par une variable aléatoire, on peut, en réalisant ds simulations avec un grand nombre de particules, observer la distribution finale (en temps long) des vitesses avec une densité donnée par Ce-2V(x)/σ2.
On se place ici dans le cas de la dimension 1. Ce code Python permet de calculer la distribution finale (en temps long) des vitesses pour un grand nombre de particules (1000 particules).
On s'intéresse via ce code Python à un système proie-prédateur avec trois espèces en compétition, sur le modère "poule-renard-vipère" (chacune des espèces est la proie d'une autre et en chasse une autre).
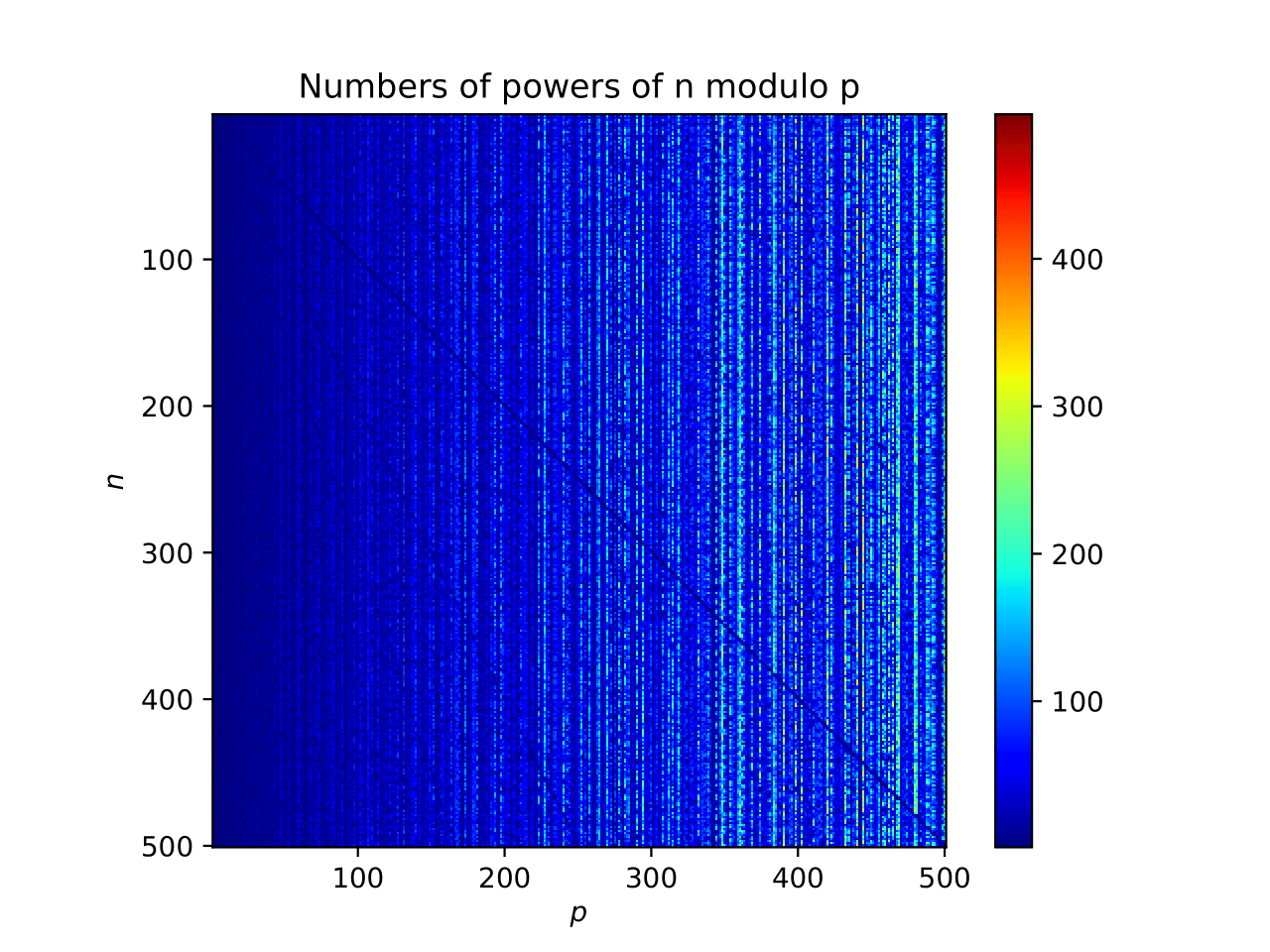
On s'intéresse ici au nombre de puissances d'un entier naturel n modulo un second entier p, c'est-à-dire quel est le nombre d'éléments de nk dans ℤ/pℤ pour tout k ∈ ℕ. Ce code Python permet d'effectuer rapidement les calculs. On observe ainsi de grandes valeurs pour certains nombres, s'avérant correspondre aux nombres premiers, augmentant avec la valeur des nombres premiers.
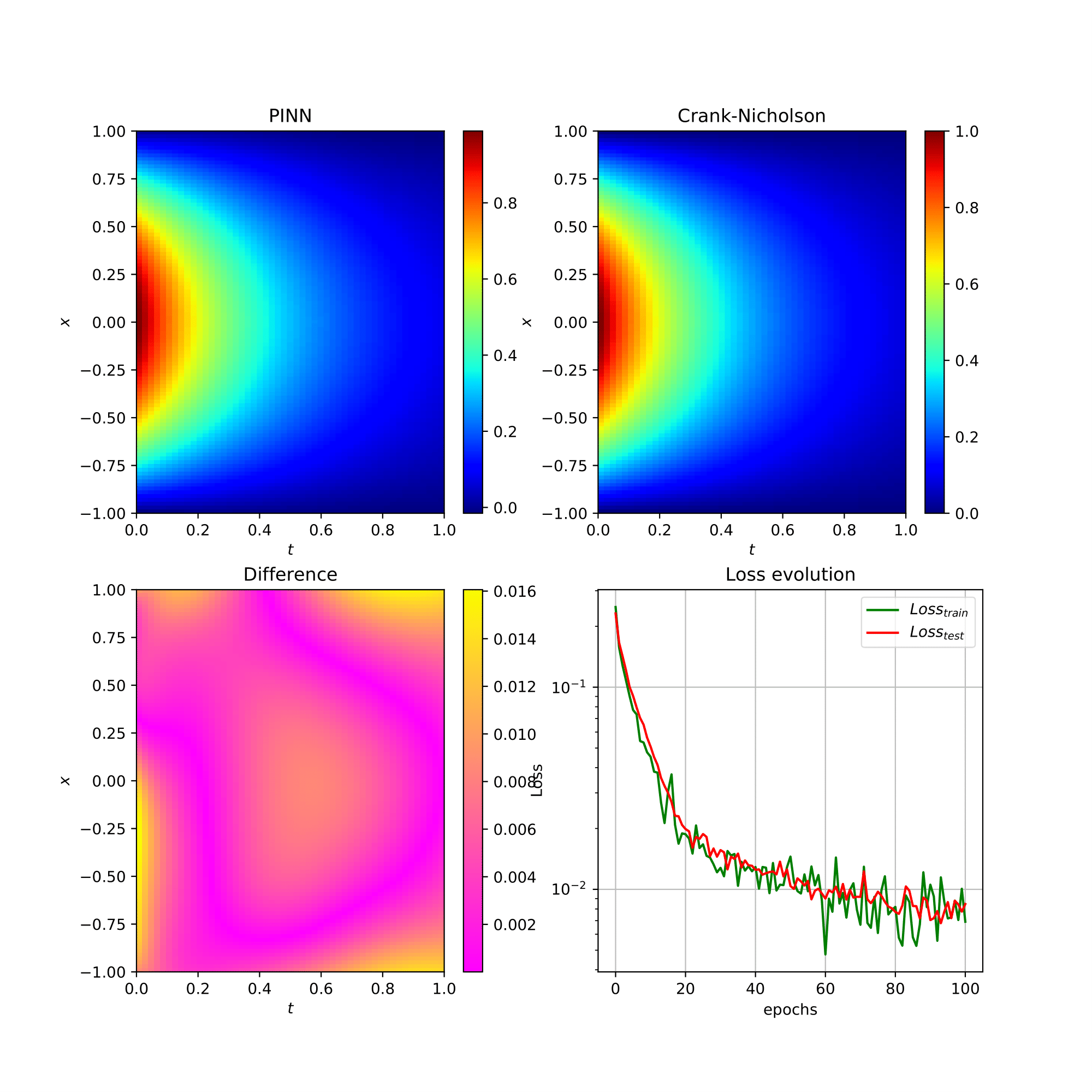
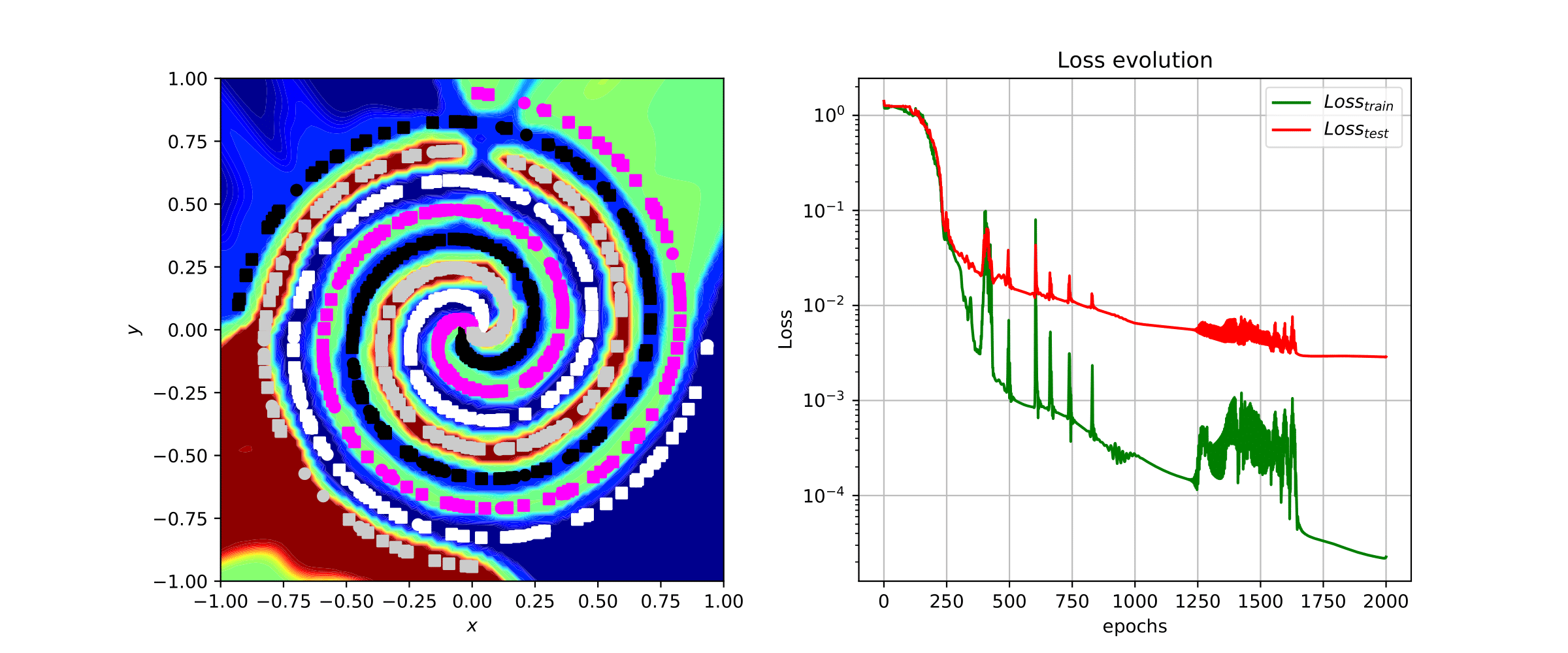
Afin de résoudre une équation aux dérivées partielles, il est possible d'utiliser les PINN's (de l'anglais Physics Informed Neural Network), ce qui permet de résoudre l'équation en une ou plusieurs dimensions, tout en ayant un domaine possédant une géométrie complexe.
On résout via ce code Python l'équation de la chaleur en une dimension d'espace ∂tu = ∂x2u sur le segment [-1,1] avec conditions de Dirichlet au bord.
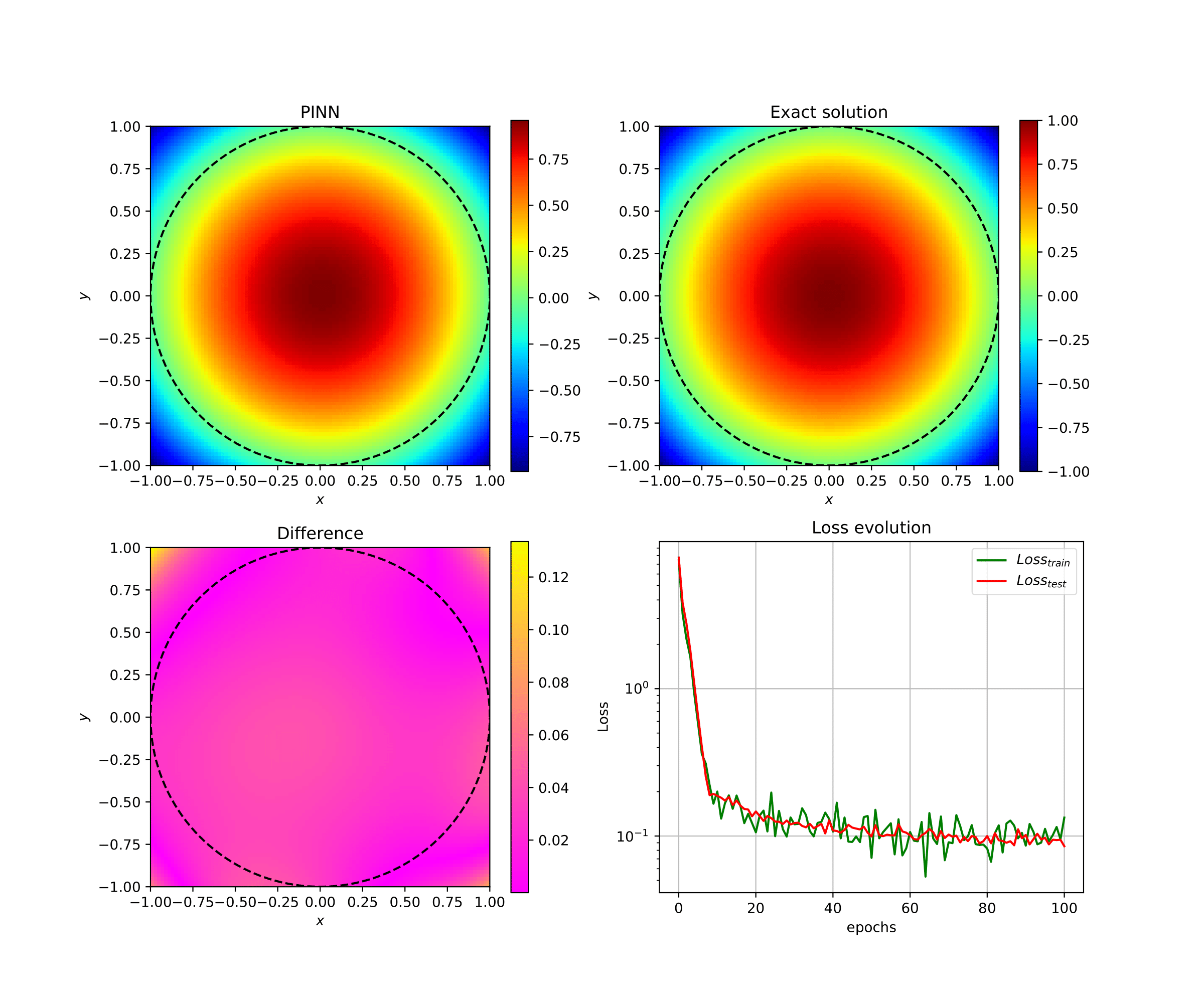
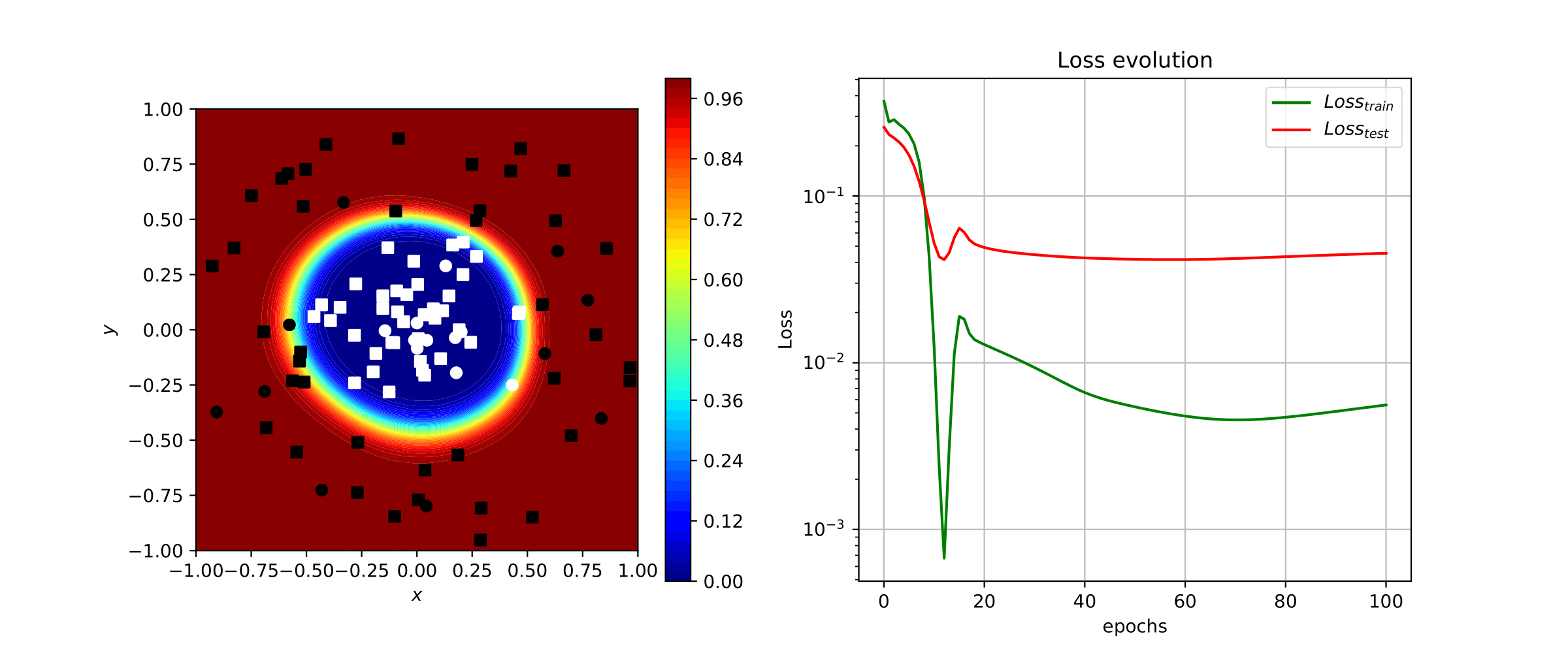
On résout via ce code Python l'équation de Poisson en deux dimensions d'espace -Δxu = 4 sur le disque unité avec conditions de Dirichlet au bord.
On résout via ce code Python l'équation de la chaleur en deux dimensions d'espace ∂tu = Δxu sur le disque unité avec conditions de Neumann au bord.
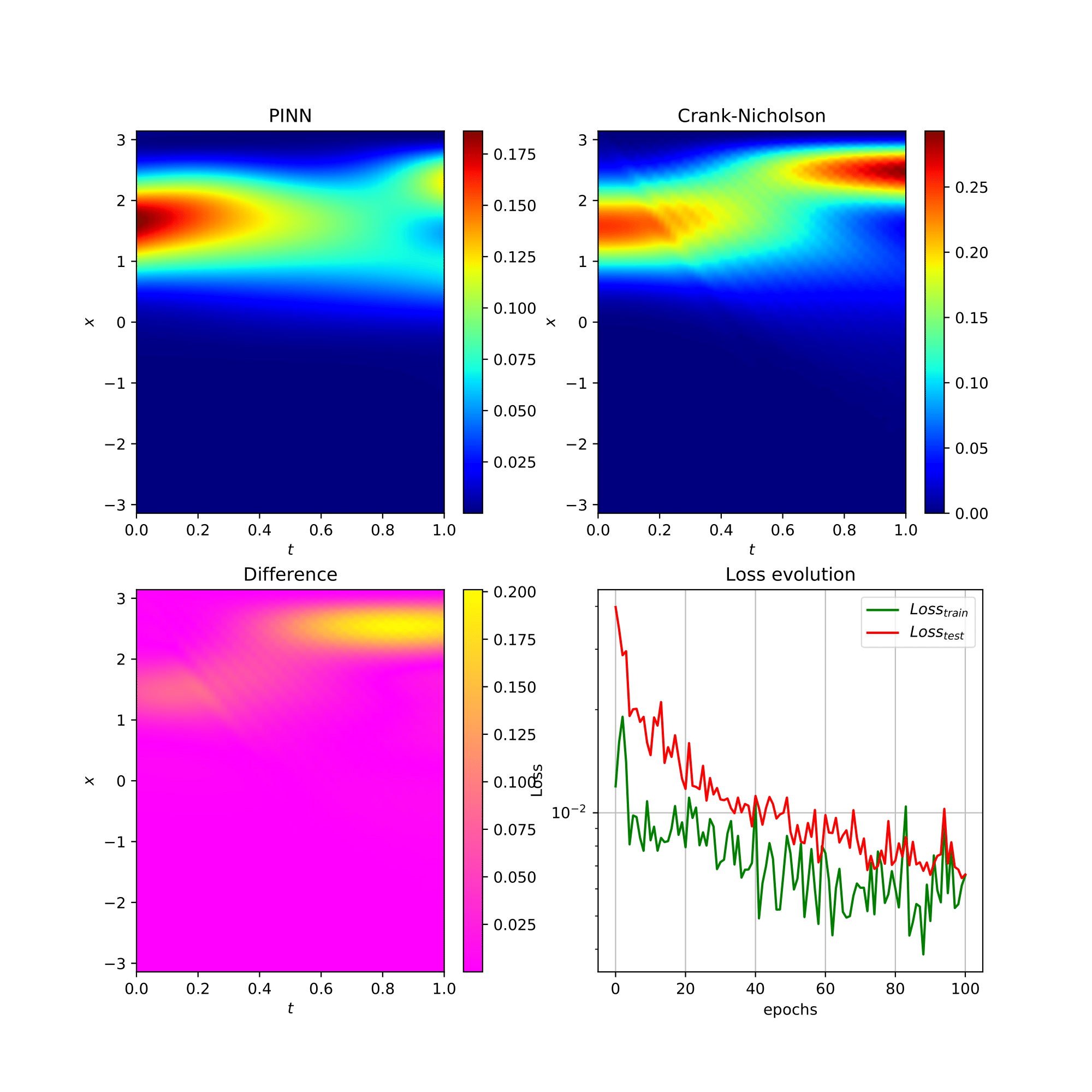
On résout via ce code Python l'équation de Schrödinger en une dimension d'espace ∂tu = i(∂x2u+x2u)/2 sur le segment [-1,1] avec conditions de Dirichlet au bord.
En Machine Learning, une application des réseaux de neurones conserne le problème de classification, qui consiste à séparer des données étiquetées en différents groupes via un apprentissage sur un jeu de données (on parle de problème de classification en apprentissage supervisé), puis à généraliser avec des données étiquetées mais inconnues. Le code Python suivant permet une première résolution de ce problème (les données sont matérialisées par des carré pour celles servant à l'entraînement ou des points pour celles servant au test, avec différentes couleurs pour chaque étiquette).
Le problème à N corps généralise l'étude du problème à deux corps, qui permet de décrire le mouvement de deux astres entre eux. Tandis que le problème à deux corps peut-être facilement étudié et donne des trajectoires d'astres plutôt prévisibles (par exemple une planète tournant autour de son étoile), le problème à trois (et N) corps donne des trajectoires cahotiques. Ce code Python permet d'approcher des trajectoires de N astres (de même masse) liés entre eux par ce problème.
Pour résoudre numériquement l'équation de transport ∂tu = c ∂xu, une méthode très connue consiste à utiliser la méthode des différences finies, qui utilise la discrétisation en temps puis en espace de l'EDP. Une fois l'opérateur ∂x discrétisé en espace, la résolution numérique de l'EDP s'apparente ainsi à la résolution numérique d'une EDO. Un premier schéma, inspiré de la méthode d'Euler Implicite, garantit la stbalilité, mais n'est que d'ordre 1 et temps et en espace, ce qui ne garantit pas une bonne erreur numérique (problème de diffusion numérique). Un second schéma, appelé schéma de Lax-Wendroff, corrige ce défaut car est d'ordre 2 en espace et en temps, mais nécéssite un peu plus de calculs.
Ainsi, nous proposons ici une méthode alternative au schéma de Lax-Wendroff, qui consiste à rechercher, pour une discrétisation en espace et en temps données, une matrice donnant le passage de la solution d'un temps t à un temps t+ht, à partir de solution exactes. Cette méthode s'inspire du Machine Learning (création de données, minimisation d'une fonction d'erreur) et permet d'éviter les calculs supplémentaires tout en réduisant le phénomène de diffusion numérique, et permet d'améliorer le schéma d'Euler Implicite (voire de concurrencer Lax-Wendroff pour des discrétisations grossières en espace). Le code Python suivant a permis de réaliser les simulations numériques.

Dans la vie courante, nous utilisons la base 10 afin d'y effectuer nos calculs. Cependant, cela n'a pas toujours été le cas. Les babyloniens utilisaient par exemple la base 60, tandis que les civilisations Mayas et Aztèques ont utilisé la base 20 et la base 12 a été largement utilisée avant la révolution (et continue plus ou moins de l'être au travers des calculs de durées). Enfin, les ordinateurs utilisent le système binaire, autrement dit, ils comptent en base 2. Ce code Python permet de donner les tables d'addition et de multiplication dans une base inférieure à 36 (limitée par les lettres de l'alphabet et les chiffres). Ci-dessous, les tables d'addition et de multiplication en base 12.


Diverses fractales ont été simulées par ordinateur.
Le flocon de Koch est une fractale construite à partir d'un triangle équilatéral auquel est ajouté au milieu de chaque côté un triangle équilatéral trois fois plus petit. On répète ce processus à chaque itération en diminuant de trois la taille des triangles ajoutés. Cette figure présente aussi la particularité d'avoir une longueur infinie tout en restant de surface finie. En effet, bien que bornée dans le plan, la longueur est multipliée par 4/3 à chaque itération, d'où une longueur infinie. Les itérations successives sont calculables via ce code Python.






L'éponge de Menger est une structure fractale construite via des itérations successives en suivant ce procédé: A l'étape 0, on considère un cube, que l'on subdivise en 27 petits cubes identiques. On supprime les 7 cubes ne rencontrant pas une arrête du cube initial, ne donnant que 20 cubes. A l'itération 1, on répète ce procédé sur les 20 cubes, donnant 400 petits cubes à la seconde itération, et on peut répéter le procédé jusqu'au nombre d'itérations souhaité.
Au fil des itérations, on peut voir que le cube initial se creuse. En effet, son volume est multiplié par 20/27 à chaque itération, pour au final donner une éponge de Menger ayant une mesure de Lebesgue nulle. Les itérations successives sont calculables via ce code Python. Du fait de la multiplication par 20 du nombre de cubes à traiter à chaque itération, la temps de calcul augmente considérablement à partir de seulement trois-quatre étapes de construction.





La courbe de Hilbert 3D est une version en trois dimensions de la courbe de Hilbert, c'est-à-dire qu'il s'agit d'une fonction f : [0,1] → [0,1] × [0,1] × [0,1] surjective, autrement dit, sa courbe représentative remplit tout le cube. Cette fonction peut s'approcher via une suite de fonctions comme on peut le voir par la suite.
Tout comme dans le cas 2D, au bout d'un nombre suffisant d'itérations, on peut voir que la courbe occupe de plus en plus de place et semble remplir le cube, ce qui au premier abord peut sembler surprenant, car une courbe n'a pas de volume, tandis qu'un cube en a un. Les itérations successives sont calculables via ce code Python.




La courbe de Hilbert est un exemple de courbe remplissante, c'est-à-dire qu'il s'agit d'une fonction f : [0,1] → [0,1] × [0,1] surjective, autrement dit, sa courbe représentative remplit tout le carré. Cette fonction peut s'approcher via une suite de fonctions comme on peut le voir par la suite.
Au bout d'un nombre suffisant d'itérations, on peut voir que la courbe occupe de plus en plus de place et semble recouvrir le carré, ce qui au premier abord peut sembler surprenant, car une courbe n'a pas de surface, tandis qu'un carré en a une. Les itérations successives sont calculables via ce code Python.




La méthode de Newton, mise au point il y a plusieurs siècles, est incontournable lorsque l'on veut approcher le zéro d'une fonction. L'idée est d'utiliser une suite récurrente qui va approcher ce zéro, tant que son premier terme reste assez proche de ce dernier. Toutefois, lorsqu'une fonction possède plusieurs zéros, le choix du premier terme de la suite est important, car une légère perturbation peut faire converger la suite vers deux zéros différents. On dit alors que ces deux premiers termes appartiennent à deux bassins d'attration différents. Il est tout-à-fait possible de visualiser les bassins d'attraction d'une fonction réelle, mais également complexe, donnant ainsi des fractales, que l'on appelle fractale de Newton. Ce premier code Python permet de tester la méthode de Newton et de mettre en évidence les bassins d'attraction sur une fonction polynomiale rélle, tandis que ce second code Python permet d'étendre la méthode et la mise en évidence des bassin d'attraction à des fonctions polynomiales complexes (holomorphes). Ce travail a fait l'objet d'une présentation lors des 5 Minutes Lebesgue (Centre Henri Lebesgue, Université de Rennes) le 16 Mai 2023, dont le support de présentation se trouve ici.



Ce code Python permet dans un premier temps la création d'un Labyrinthe. La méthode utilisée est l'algorithme de Kruskal, qui consiste à casser aléatoirement des murs jusqu'à ce que toutes les cases soient accessibles les unes aux autres. Des murs supplémentaires sont ensuite abattus afin de créer un Labyrinthe complexe (plusieurs chemins joignent l'entrée à la sortie). Dans un second temps, le code va résoudre le Labyrinthe, en le parcourant depuis la sortie et en notant la distance de chaque case à la sortie. Une fois l'entrée atteinte, il ne reste plus qu'à aller vers les cases de distance de plus en plus petite pour rejoindre la sortie.
Un automate cellulaire est une grille régulière de cellules qui peut prendre un nombre fini d'états ai cours du temps (on est en temps discret). Le changement d'état d'une cellule au temps suivant se fait en fonction de son état et de celui de cellules voisines. Un automate cellulaire élémentaire regarde l'état de cellules en une dimension d'espace, valant 0 ou 1, avec une dépendance de l'état suivant chaque cellule en fonction de son propre état et de celui de ses deux celulles voisines. Il en existe 256 différents. L'un d'entre eux, permet par exemple de modéliser la surface d'un cône (animal marin). Un autre permet de reconstituer le triangle de Sierpinski, une fractale très célèbre via ce code Python.


On modélise ici l'interpolation d'une courbe fermée du plan pouvant représenter une figure quelconque via une série de Fourier. Le nombre de paramètres peut se trouver réduit, ce qui allège le stockage. Ce code Python permet de modéliser une telle interpolation.
Ce programme permet de simuler des équations différentielles stochastiques. Un premier schéma utilisable est la méthode d'Euler Explicite, cependant, contrairement aux équations différentielles où ce schéma est d'ordre 1, l'ordre de convergence de cette méthode est ici d'ordre 1/2, ce qui impose l'ajout d'un terme correctif dans le schéma numérique, donnant le schéma de Milstein, d'ordre 1 cette fois. Le modèle simulé est le modèle de Black-Scholes, qui modélise de manière simple l'évolution du cours de la bourse.
Les illustrations représentent 100 simulations de l'EDS pour la première, et des courbes de convergence avec les deux schémas numériques proposés pour la seconde.


Les systèmes dynamiques à temps discret permettent, sous certaines conditions, de produire des suites de points modélisant différentes figures, voire certains éléments que l'on trouve dans la nature. C'est par exemple le cas de certains système dynamiques utilisant une itération aléatoire d'applications affines du plan, modélisant des fougères, appelées fougères de Barnsley (nommées en l'honneur du mathématicien britannique M.Barnsley qui les a développé). Ce programme Python permet le tracé de deux fougères. Il est possible de créér d'autres systèmes dynamiques de la même forme (tant que les applications affines mise en jeu restent contractantes).


Voici un code Python reproduisant le modèle de Vicsek, qui simule les nuées d'oiseaux et leur tandance à se regrouper et voler dans la même direction lorsqu'ils sont proches.
Ce projet a été mené en coopération avec une étudiante de géologie dans le cadre de séances de soutien afin de modéliser divers phénomènes géologiques.
Ce projet présente la méthode des éléments finis de Lagrange en une dimension d'espace en introduisant le principe de cette méthode, puis l'équation de Poisson est étudiée. Des résultats de convergence sont ensuite démontrés et illustrés via des simulations numériques. Enfin, la méthode à pas adaptatif, qui permet de raffiner le maillage à un endroit précis, est abordée.
Voici les documents associés au projet: